Here’s a fun little problem. It’s from the latest MIT magazine:

M/J3. Tom Harriman wants you to divide a square of side length into four equal-area pieces so that the sum of the lengths of the boundaries is minimized. Hint: It is easy to get four side squares with total boundary But you can do better.

The first thing to notice is that the outside of the square will always be counted in the total boundary, so we just need to focus on minimizing the length of the cuts on the inside. In other words, we would like to find some interior cuts which create equal-area pieces but have total length less than It seems impossible, at first, to beat two straight lines. One might think that we must therefore try curved lines. Maybe that works, but I did not find it to lead anywhere. Well, this is a devious problem. Let’s take a look at a possibility anyways, though.

It is easy to see how we must construct such a picture, since each piece must have area (As a result, the radius of each quarter-circle is It turns out that the total interior lengths sum to However, it was unclear at first glance whether the sum is less than or greater than and this is because the inside diagonal is shared when we consider the cuts from left to right and up to down. Although this example doesn’t work, we can use this insight!

Let’s now revert back to straight lines, since they may work better. Let’s try to replace each of the four “curved segments” with straight lines and see if we can fiddle around with the length of the middle line to make it work. For example, something like this.

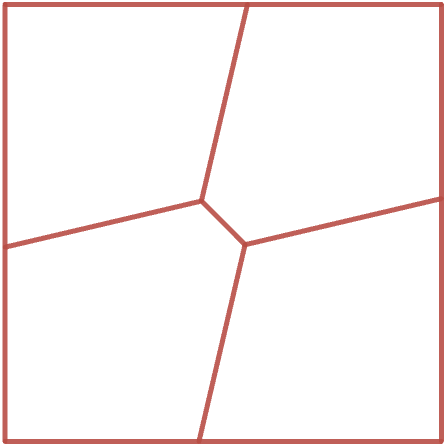
There is one parameter we can change within our restrictions. Notice that if we make the center diagonal longer, the other lines will be forced to move in order to maintain the equal area pieces, and vice versa. Suppose the side length of the right triangle (as below) made by the center diagonal has length

Since each of the regions has area 1, we know that if we cut the region on the top left in half to form two identical triangles, their regions will have area

Following the diagram, if we use the side that lies on the top edge of the square as a base for the triangle, we have where So solving in terms of we get Now let’s find the lengths of the interior lines in terms of a, so that we see if this works for some a. We can calculate the length of the longer inner segment through the Pythagorean Theorem. The base is and the height is so the length is We have four of these and one diagonal of length so our total interior length is:

We know that a can take values strictly between and (but between and realistically). Plotting this on Desmos, we find that the local minima within this range is at with a total area of

So, we’ve found an arrangement where the total interior lengths add up to less than ! Below is a depiction of the optimal solution given the lengths:

Here is a slider I made, and you can play around with changing the value of .

This solution is better, as the question prompted… But I’m not sure if this is the optimal solution. I couldn’t think of anything better, but I’ll be interested to see if there is one!

 

Source: Puzzle corner’s Problem M/J3 of MIT News May/June 2023 edition.